I’ve stolen the title of a very interesting post by Andrew Bacon over at Possibly Philosophy. He considers a situation where there will be infinitely many coin flips occurring between noon and 1 pm, but instead of getting faster and faster, they’re getting slower and slower. In particular, one coin flip occurs at 1/n past noon for each integer n. He shows that there exists a strategy for guessing, where each guess may use information about how previous coin flips have come up (which sounds like it should be irrelevant, because they’re all independent 50/50 flips), such that one is guaranteed to get all but finitely many of the guesses correct. In particular, this means that although there is no first flip, there is a first flip on which one gets an incorrect guess, so up to that point one has successfully guessed the result of infinitely many independent fair coin tosses.
Check out his post to see the description of the strategy, or work it out yourself, before going on.
Anyway, I managed to figure this out, only because it’s formally identical to a game with colored hats that I had discussed earlier with math friends. But I think Andrew’s version with the coin flips is somehow even more surprising and shocking!
He begins his discussion with a discussion of a very nice paper by Tim Williamson showing that allowing infinitesimal probabilities doesn’t get us around the requirement that the probability of an infinite sequence of heads be 0. (Coincidentally, I’m currently working on a paper extending this to suggest that infinitesimal probabilities really can’t do much of anything useful for epistemological purposes.) Andrew concludes with a bit more discussion of these probabilistic issues:
Now this raises some further puzzles. For example, suppose that it’s half past twelve, and you know the representative sequence predicts that the next toss will be heads. What should your credence that it will land heads be? On the one hand it should be 1/2 since you know it’s a fair coin. But on the other hand, you know that the chance that this is one of the few times in the hour that you guess incorrectly is very small. In fact, in this scenario it is “infinitely” smaller in comparison, so that your credence in heads should be 1. So it seems this kind of reasoning violates the Principal Principle.
I was going to leave this following series of remarks as a comment, but it got bigger than I expected, and I liked this puzzle so much that I figured I should point other people to it in my own post anyway. So I don’t think that this puzzle leads to a violation of the Principal Principle. (For those who aren’t familiar, this principle comes from David Lewis’ paper “A Subjectivist’s Guide to Objective Chance” and states the seeming triviality that when one knows the objective chance of some outcome, and doesn’t know anything “inadmissible” specifically about the actual result of the process, then regardless of what other historical information one knows, one’s degree of belief in the outcome should be exactly equal to the chances. The only reason this principle is normally in dispute is in terms of figuring out what “inadmissible” means – if we can’t make sense of that concept then we can’t use the principle.)
The set of representatives involved in picking the strategy is a non-measurable set. To see this, we can see that the construction is basically a version of Vitali’s construction of a non-measurable set of reals. The only difference is that in the case of the reals we make use of the fact that Lebesgue measure is translation invariant – here we make use of the fact that measure is invariant under transformations that interchange heads and tails on any set of flips. Instead of the set of rational translations, we consider the set of finite interchanges of heads and tails. (This argument is basically outlined in the paper by Kadane, Schervish, and Seidenfeld, “Statistical Implications of Finitely Additive Probability”, which I’ve been working through more carefully recently for another paper I’m working on.)
This suggests to me that the set of situations in which you make the wrong guess on flip n may well be unmeasurable as well. (I haven’t worked out a proof of this claim though. [UPDATE: I have shown that it can sometimes be measurable depending on the strategy, and I conjecture that whenever it is measurable, it will have probability 1/2. See the comments for the argument.]) So from the outset (before the game starts) it looks like you can’t (or perhaps better, don’t) assign a credence to “I will make the wrong choice on flip n”. However, once it’s actually 1/n past twelve, you’ve got a lot more information – in particular, you know the outcomes of all the previous flips. I suspect that conditional on this information, the probability of making the wrong choice on flip n will just be 1/2, as we expect. (Of course, we have to make sense of what the right conditional probability to use here is, because we’re explicitly conditionalizing on a set of probability 0, as per Williamson.) Thus, there’s no violation of the Principal Principle when the time actually comes.
However, there does appear to be a violation of a principle called “conglomerability”, which is what my interest in the Kadane, Schervish, and Seidenfeld paper is about. One version of this principle states that if there is a partition of the probability space, and an event whose probability conditional on every event in this partition is in some interval, then the unconditional probability of that event must also be in this interval. In this case we’ve got a partition (into all the sequences of flips down to the nth) and the probability of guessing wrong conditional on each event in that partition is 1/2, and yet I’ve said that the unconditional probability is undefined, rather than 1/2.
I think I have a defense here though, which is part of my general defense of conglomerability against several other apparent counterexamples (including some in this paper and others by Seidenfeld, Schervish, and Kadane, as well as a paper by Arntzenius, Elga, and Hawthorne). The problem here is that the event whose unconditional probability we are interested in is unmeasurable, so it doesn’t even make sense to talk about the unconditional probability. In the case of the conditional probabilities, I’d say that strictly speaking it doesn’t make sense to talk about them either. However, conditional on the outcome of the flips down to the nth, this event is coextensive with something that is measurable, namely “the coin will come up heads” (or else perhaps, “the coin will come up tails”), because the sequence of flips down to that point determines which outcome I will guess for that flip. Thus these events have well-defined probabilities.
The only reason this situation of an apparent violation of conglomerability emerges is because we’re dealing explicitly with unmeasurable sets. However, I’m only interested in the application of probability theory to agents with a certain type of restriction on their potential mental contents. I don’t want to insist that they can only grasp finite amounts of information, because in some sense we actually do have access to infinitely many pieces of information at any time (at least, to the extent that general Chomskyan competence/performance distinctions suggest that we have the competence to deal with infinitely many propositions about things, even if in practice we never deal with extremely large sentences or numbers or whatever). However, I think it is reasonable to insist that any set that an agent can grasp not essentially depend on the Axiom of Choice for the proof that it exists. Although we can grasp infinitely much information, it’s only in cases where it’s nicely structured that we can grasp it. Thus, the strategy that gives rise to this problem is something that can’t be grasped by any agent, and therefore this problem isn’t really a problem.
[…] A couple of links September 26, 2008 Firstly, Kenny Easwaren has a great post on the coin tossing puzzle I presented a few days ago. This is something I’ll probably be […]
Hi Kenny,
Thanks – that’s a lot for me to think about there! When you say “the set of situations in which you make the wrong guess on flip n may well be unmeasurable” do you mean the set
where f is the choice function for the strategy and pi_n returns the nth coordinate in a backwards omega sequence?
I think that is unmeasurable, if the range of f is. But but the probability of that is only sensibly taken to be your credence that you’ll get the nth guess right if you are certain that you are going to use f as your strategy.
So two things to note. Firstly, what is your credence that you’ll get guess n right before you have chosen a particular strategy, but given that you know you’re going to chose a strategy that will get you cofinitely many right? If that’s all you know, I think that your credence should be 1. (Regarding the Principal Principle, perhaps this is inadmissible evidence – it’s almost like you’re getting information about how the future is going to turn out, not from a time traveller, but by running the mathematical argument.)
Secondly, in my post I had it in mind that we evaluate the agents credence after the tosses from omega to n+1 had been performed, but before the nth coin toss. You say her credence should be 1/2. And I think I might be swinging in that direction. But the other line of reasoning is also quite compelling: that you’re going to be correct cofinitely times within the hour, it seems very likely you’ll be correct on this go. But my point is, your credence that you’ll get toss n right will be equal to your credence that toss n will be heads, or equal to your credence that toss n will be tails (depending on the representative.) And in either case, you would expect it to be measurable (so very much unlike the case before any coins have been tossed, but after a strategy has been picked.)
BTW, just to make sure I’m following, what did you mean when you said that the “measure is invariant under transformations that interchange heads and tails on any set of flips.”
Yes, that’s the set I meant.
For the “invariant under transformations” what I mean is this. Consider any measurable set of sequences of coin tosses. Now specify some set
of sequences of coin tosses. Now specify some set 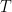 of natural numbers. Let
of natural numbers. Let 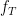 be the function that takes any sequence
be the function that takes any sequence  to the sequence that differs from that one exactly on the flips whose index is in
to the sequence that differs from that one exactly on the flips whose index is in 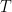 . Let
. Let 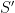 be the set
be the set 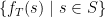 . Then the measure of
. Then the measure of 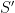 equals the measure of
equals the measure of  . This is exactly analogous to “translation invariance” for Lebesgue measure, though I suppose it’s slightly less involved to define a translation of a set than to define the transformation of a set by one of these functions.
. This is exactly analogous to “translation invariance” for Lebesgue measure, though I suppose it’s slightly less involved to define a translation of a set than to define the transformation of a set by one of these functions.
That’s an interesting question about what the credence should be before you’ve specified the choice function. I’ll have to think more about what goes on then.
However, I no longer think the set I talk about is always going to be unmeasurable. In fact, I can show that in some cases it is measurable, with probability 1/2.
Note that the strategy involves picking a representative from each of the equivalence classes, where two sequences are equivalent if they differ at only finitely many points. For each equivalence class, and each n, there are representatives of that equivalence class where the nth flip comes up heads, and representatives where the nth flip comes up tails. By the Axiom of Choice, instead of picking an arbitrary representative of each equivalence class, we can actually pick an arbitrary representative of each equivalence class where the nth flip comes up heads. If this is our strategy, then we know in advance that our guess on the nth flip will be heads, and we have credence 1/2 that the nth flip will come up heads, so the credence that we’ll be right this time is 1/2.
Of course, this relies on a peculiarity of this particular strategy. But I think now I’m convinced that the probability of this relevant set will be 1/2 whenever it is measurable. (I think it’ll be measurable iff the sets “I guess heads on flip n” and “I guess tails on flip n” are measurable, and each of those is independent of flip n, so multiplying and adding we get answer 1/2. So I just need to confirm that it’s measurable iff those two sets are measurable.)
At any rate, once you’ve already observed cofinitely many flips, and guessed on them, what you now know is that you have n flips remaining, and that you’ll get only finitely many of them wrong – which doesn’t seem to constrain your credence that you’ll get this next one wrong at all. It’s only when you already know that you’ll get cofinitely many right, but don’t yet know anything about which ones those are, that I think it looks convincing to say that your credence of getting any particular flip right will generically be 1.
Hi Kenny,
Thanks, that answered some of my questions. Note that, if p := p_n = “you get guess n right” = {a | pi_n(a) = pi_n(f([a]))}, then ~p is just a translation of p in the sense that you just defined for me. Namely the translation that just flips the nth coordinate (because flipping one coordinate keeps us in the same equivalence class.) So Pr(p) = Pr(~p) by your translation invariance principle, and since they are exclusive and exhaust the space we have Pr(p)=1/2 (but only *if* p is measurable.)
So maybe you can help me out here. Surely we can show that there must be *some* n for which p_n is unmeasurable? Otherwise we’d have (1) they’re all measurable (2) if they’re measureable then the probability is 1/2, but (3) each possible sequence lies in only finitely many of the propositions p_n.
I see what you mean about the credence immediately before the nth flip. It’s just the situation is so similar to situations the the principal principle doesn’t apply, e.g. if a time traveller tells you that the coin will land heads 9 out of ten times in the next hour, even though you know its fair. Ok, I know that in the infinite case your credences aren’t constrained by the information in the same way as they are here, but it’s enough to shake my faith that the PP will still apply here.
I get the feeling that your credence in p_n before the strategy has been decided has to be 1, provided you don’t prefer any strategy. That would make trouble for your conglomerability principle. I’ll have to think about it some more though.
Ah, that argument is good. And of course, the translation invariance is there only because the coin is supposed to be a fair coin.
I think the argument can be generalized even to the case where you haven’t yet chosen the strategy. In this case of course the space is no longer just the set of sequences, but the set of pairs consisting of a sequence of flips together with a function for the strategy. I don’t know how we would distribute credences over the strategies, but no matter which distribution we use, if we do it in a way that’s independent of the distribution over the sequences of flips, then the same argument about translation invariance shows that the credence in p_n must still be 1/2 (if it’s measurable – but in this case it seems much more plausible that it must not be measurable, approximately for the reasons you suggest).
Anyway, given a strategy, we can again use translation invariance to find the joint distribution of a finite set of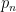 . For any set of k of these, consider all the
. For any set of k of these, consider all the 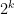 conjunctions of the
conjunctions of the 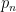 and their negations, and note that all of these events are just translations of the others, and thus must have the same probability, so the probability of any conjunction of k of them is just
and their negations, and note that all of these events are just translations of the others, and thus must have the same probability, so the probability of any conjunction of k of them is just 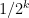 . In particular, this means that they are pairwise independent.
. In particular, this means that they are pairwise independent.
By the second Borel-Cantelli lemma, if there is a sequence of pairwise independent events, and the sum of their probabilities is infinite, then with probability 1, infinitely many of them occur. If there were an infinite set of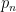 that were all measurable, then by the above result, their negations would be pairwise independent and their probabilities would sum to infinity, and thus infinitely many of them would occur. But we have proven that only finitely many of them occur. Thus, there must not be infinitely many of them that are measurable.
that were all measurable, then by the above result, their negations would be pairwise independent and their probabilities would sum to infinity, and thus infinitely many of them would occur. But we have proven that only finitely many of them occur. Thus, there must not be infinitely many of them that are measurable.
Of course, I’d be much more convinced of this result if I could prove somehow more directly that one of these sets must be unmeasurable. But the reasoning so far all looks good, and it seems to entail that all but finitely many are unmeasurable, which is basically what I expected. This argument seems to work both before and after choosing a strategy.
If we assume a further sort of permutation invariance, namely that the probabilities are the same if you permute any finite set of indices (both in the sequence of flips and in the choices of representatives – I think this must be part of what you mean by “you don’t prefer any strategy”) then the fact that all but finitely many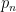 must be unmeasurable before you’ve chosen a strategy means that all of them must be unmeasurable before you’ve chosen a strategy.
must be unmeasurable before you’ve chosen a strategy means that all of them must be unmeasurable before you’ve chosen a strategy.
Ah, nice! Thanks for sorting that out. I didn’t know this lemma. Also, for some reason I thought the argument wouldn’t carry over to the sequence function pairs.
I’m beginning to get a feel for the structure of the problem now (although it seems my intuitions are appalling.)
Actually, I was wondering how things would look if you didn’t do it with fair coins. Although translation invariance would fail, your finite permutation invariance would stick. But it seems odd that a lot of things might turn out differently if the coin wasn’t fair.
It is indeed true that the set where you guess n right is measurable iff the set where you guess n is heads and the set where you guess n is tails are measurable. Indeed, if x is your nth guess and y is the actual value,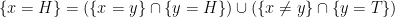 , and
, and 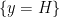 and
and 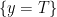 are measurable.
are measurable.
If the measure is just defined on the Borel algebra of events here (that is, the smallest σ-algebra containing all events defined only in terms of the results of finitely many coin flips) then changing the probabilities of the events doesn’t change which ones are measurable, so it shouldn’t matter whether we use a fair or unfair coin, at least in terms of which sets are measurable. As far as the actual probability of having guessed right on flip n, I think that when this event is measurable, its probability will have to be between p and 1-p, where p is the probability of heads on any given flip.
If we want the measure to be more “Lebesgue-type” rather than “Borel-type”, then it’s probably a bit harder to show that the relevant events are unmeasurable, but it should still probably work out. Certainly the Borel-Cantelli argument will still work, because there is a constant positive lower bound on the probabilities.
And Eric – thanks for the confirmation there. I’ve taken the liberty of converting your pseudo-LaTeX into actual LaTeX (on WordPress blogs you can use LaTeX math mode, just that the first dollar sign has to be followed by the word “latex”).
[…] Kenny Easwaren* has a fun post on propositions that cannot be assigned credences. See Guessing the result of infinitely many coin tosses. […]
“He shows that there exists a strategy for guessing, where each guess may use information about how previous coin flips have come up”
There can be no strategy to guess the next coin flip, the next coin will never care how the previous coins landed. If it did, it wouldn’t be a random flip.
The logical error is in assuming that a part cares about the whole.
“the requirement that the probability of an infinite sequence of heads be 0.”
The probability of a series of n flips having all heads approaches zero as n goes to infinity. Although the probability of an infinite sequence of heads goes to zero, one still must consider the case in which an infinite number of coin flips results in all heads. Think in terms of multiple universes. For the nth flip, the universe splits into two, one gets a heads and one a tails. But there is always a universe that has all heads. Extending n to infinity requires considering the universe with all heads. Ignoring this special case, or any other special number of heads or ratio of heads to tails, results in weird results.
About the strategy – if you read the description of the puzzle and the solution, there is in fact a strategy that guarantees that one gets all but finitely many guesses correct. There’s no strategy that guarantees getting all the flips correct. The part doesn’t care about the whole, but you can check that as constructed, the solution to the puzzle works. It gives no guarantee of being any better than 50/50 on guessing an individual flip, but the strategy as a whole guarantees that overall one gets only finitely many guesses wrong. There’s no logical error.
I agree that one must consider the case in which an infinite number of coin flips results in all heads. But that doesn’t mean that the probability of this situation is non-zero. You’re confusing probability 0 with impossibility, which are two distinct notions.
So I admit to not being an expert, and what expertise I do have is somewhat rusty, but this argument doesn’t seem to work to me.
To break the argument into pieces I understand, the set of times at which we flip the coin is a well ordered set, we can choose a strategy (if we grant the axiom of choice) that makes finitely many mistakes at n=1, and it’s obvious that if we have a strategy for n, the same strategy will work for n+1, so transfinite induction gives us that we can choose a strategy for any n.
What I don’t follow is how we make the jump from being able to choose a strategy for any n to being able to choose a strategy before an infinite number of mistakes has been made. It seems to me that this is like arguing that since for any n, the subset of the sequence 1/i up to and including 1/n has an upper bound, the whole sequence must have an upper bound.
So let me know if I’m missing anything.
Ohh, and hi, Kenny!
I just realized I was being silly above – plain old regular induction is sufficient since we’re dealing with a countable set, and being well ordered is true, but quite superfluous (I haven’t done this stuff in more than 6 years). Still, I don’t see how the last step works!